CG-01: Object Modeling

简单介绍了对象建模的几种方法与技术，包括从二维图形绘制到三维点云、多边形网格、分割曲面，以及隐式与参数化表面的应用，同时还简述了构造实体几何 (CSG) 和分形的特性及其构建方式。

CG-01 对象建模

1. 二维绘图 (2D Drawing)

二维绘图是将对象转换为像素模式并更新帧缓冲区中的对应像素。

• 直线绘制
  • 使用算法（如Bresenham算法）优化像素选择，通过整数运算高效绘制直线。
  • 判断线段与像素的接近程度，选择最接近的像素进行着色。
• 圆形绘制
  • 通过对称性减少计算量，逐步绘制圆的像素。
• 区域填充
  • Flood-fill算法：递归填充区域，分为4方向和8方向填充。
  • 检查当前像素是否为边界颜色或填充颜色，若不是则填充并递归处理相邻像素。

2. 三维点云 (3D Point Clouds)

三维点云是无结构的三维点样本集合，每个点包含几何信息（如坐标）及其他属性（如颜色、法向量）。

数据采集方式：

• 激光雷达（Lidar）：通过红外光脉冲测量距离。
• 结构光：通过投影光栅图案获取深度信息。
• 多视图计算机视觉：从多个视角重建三维点云。

优势：

• 实时采集：适合实时应用（如自动驾驶）。
• 无需拓扑信息：点云本身不包含连接信息，处理简单。

劣势：

• 几何计算困难：缺乏拓扑结构，难以直接进行表面重建。
• 拓扑连接信息缺失：需要额外处理以生成网格或其他结构。

特殊处理：

• 结构化点云：将点云表示为二维图像，利用成熟的图像处理技术进行分析。

3. 多边形网格 (Polygon Meshes)

多边形网格通过顶点 (V)、边 (E)、面 (F) 表示多面体对象的形状。

• 每个面可以通过定义顶点的排列顺序来指定方向。

  • 方向可以是**逆时针 (counter-clockwise) 或顺时针 (clockwise) **。

• 方向决定了面的法向方向。通常，逆时针顺序是“正面”。

• 可以使用右手法则 (Right-hand rule) 来进行判断。

• 如果一个网格的所有面都能保持一致的方向（全部逆时针或全部顺时针），并且每条边在其相邻的两个面中有相反的方向，则该网格是**可定向的 (orientable) **。

• 并非所有网格都是可定向的。

  • 例如：
    • 莫比乌斯带 (Möbius strip)
    • 克莱因瓶 (Klein bottle)
    • ……

• 欧拉公式：
  对于闭合无孔的凸多面体，顶点数 V、边数 E、面数 F 满足关系：

  

对于具有孔洞或边界的网格，公式需根据曲面属 (Genus) 和边界调整。

• 曲面属 (Genus)：
  定义为：可以在曲面上绘制的不相交的简单闭合曲线的最大数量，并且这些曲线不会将曲面分割为多个部分。

  表示曲面的孔洞数量，影响欧拉公式的计算。

  

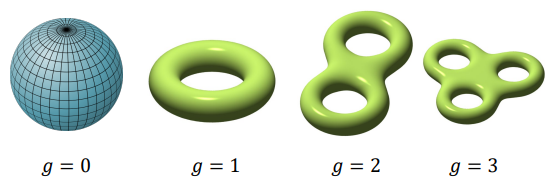
• 对于具有曲面属 g 的封闭且可定向的流形网格，顶点 (V)、边 (E) 和面 (F) 的数量之间的关系, 由欧拉公式给出：, 其中 被称为欧拉示性数 (Euler characteristic)。

• 对于具有曲面属 g 和 b 个边界的可定向流形网格 (orientable manifold mesh)，欧拉公式为：

数据结构：

• 面-顶点表：记录顶点坐标和面信息。
• 半边结构：支持高效的拓扑操作。
• 其他结构：如翼边结构、四边结构等。

优势：

• 支持任意几何和拓扑结构。
• 可表示锐边特征，支持自适应细化。
• 渲染效率高。

劣势：

• 平滑变形困难。
• 多边形边界在近距离观察时可能明显。

4. 分割曲面 (Subdivision Surfaces)

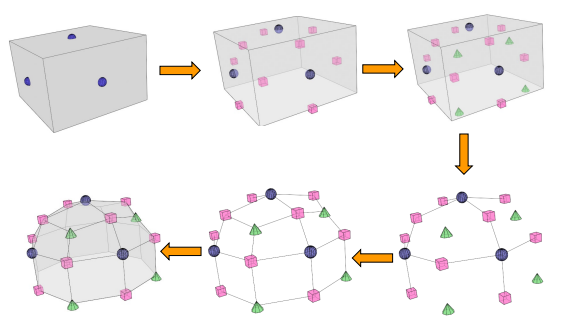
分割曲面通过递归细化生成平滑曲面。

常见方法：

• Catmull-Clark算法：适用于四边形网格，生成平滑曲面。

  

• Loop算法：适用于三角形网格。

• Doo-Sabin算法：生成平滑的多边形曲面。

• Butterfly算法：插值细分算法。

应用：

• 复杂曲面建模，适合需要高平滑度的场景。

5. 隐式表面 (Implicit Surfaces)

隐式表面通过隐式函数 定义，表示满足该方程的点集合。

特性：

• Signed Distance Field (SDF)
  • 定义点到表面的最近距离。
  • 表示表面， 表示在内部， 表示在外部。

优势：

• 高效判断点是否在表面内。

劣势：

• 难以生成表面上的具体点。
• 难以拼接多个隐式表面并保持连续性。
• 难以表示隐式表面的有限部分。

6. 参数化表面 (Parametric Surfaces)

参数化表面通过参数化方程定义，通常使用两个参数 s,t 控制表面形状。

参数化曲线 (三次参数多项式)

• U 是一个 1×4 的参数矩阵，形式为：

  

  其中

• P 是一个 4×1 的矩阵，称为几何矩阵 (geometry matrix)：

  

  它表示一组控制点，用于操控曲线的形状。

• M 是一个 4×4 的矩阵，称为基矩阵 (basis matrix)：
  它定义了曲线的基本属性，例如曲线的类型、控制点的影响区域，以及曲线是否通过两个端点的控制点。

• 假设 p0(x0,y0)、p1(x1,y1)、p2(x2,y2)、p3(x3,y3) 是四个控制点。给定基矩阵 M 的值，我们可以通过改变参数 u 的值，计算出曲线上任意点的 x 和 y 坐标，生成曲线图形。

  

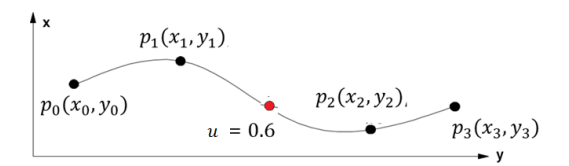
参数化曲面 (Parametric Surfaces)

• S 和 T 是参数 s 和 t 的 1×4 矩阵，形式为：,, 其中 。

• P 是一个 4×4 的矩阵，称为几何矩阵 (geometry matrix)。
  它是一组控制点的集合，用于操控曲面形状。

• M 是一个 4×4 的矩阵，称为基矩阵 (basis matrix)。
  它定义了曲面的基本属性，例如：曲面的类型、每个控制点的影响范围，以及曲面是否通过两端的控制点。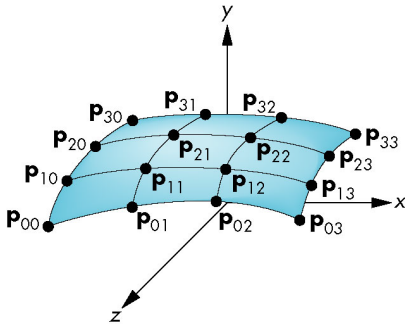

  

优势：

• 易于实现平滑变形，通过修改控制点即可调整表面形状。

劣势：

• 渲染开销较高，需要对每个参数组合进行计算。

7. 体素表示 (Voxel Representation)

没讲

体素是三维像素，用于表示对象的体积。

特性：

• 适合体积建模和体绘制。
• 常用于医学成像、地形建模等领域。

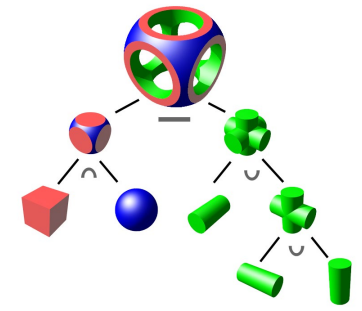
8. 构造实体几何 (Constructive Solid Geometry, CSG)

通过布尔操作（如并集、交集、差集）组合简单对象生成复杂实体。

关键操作：

• 并集 (Union)：合并两个对象。
• 交集 (Intersection)：保留两个对象的公共部分。
• 差集 (Difference)：从一个对象中减去另一个对象。

优势：

• 操作可逆，易于修改。
• 适合复杂实体的建模。

劣势：

• 修改后需重新计算所有操作。
• 计算开销较大。

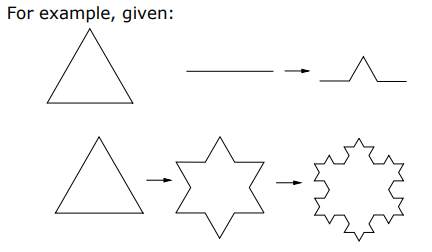
9. 分形 (Fractals)

分形对象具有自相似性，适用于自然场景（如山脉、树木、海岸线等）的建模。

生成方法：

• 通过递归函数生成细节。
• 引入随机因子（如随机调整宽度、高度、位置）以提高真实感。

优势：

• 生成细节丰富的对象。

劣势：

• 无限分辨率的细节可能不符合真实物体的特性。